2 条题解
-
1
前言
或贪心或 dp 地做最优解,或 dp 或二分地解决单调性问题,dp 或组合数学地做计数,或 dp 或数学地做构造,或 dp 或搜索地做图论,或 dp 或数据结构地做可行性,或 dp 或唉声叹气地活着,我们活在 dp 里,当然,这题的 dp 含量很低,只有求深度。
思路
清新图论题。
首先的首先,本题解节点编号为 ,代码中已经做了处理。
首先,实际上,对于所有不影响最短路的边,都是选不选都可以,设这种边的数量为 ,则答案为 。
那么接着我们来讨论哪些边不影响,显然给定的图是一颗树,那么我们让 号点为根,节点深度 就是到 号点的距离减 ,这里不影响答案,我们来看样例 的树。
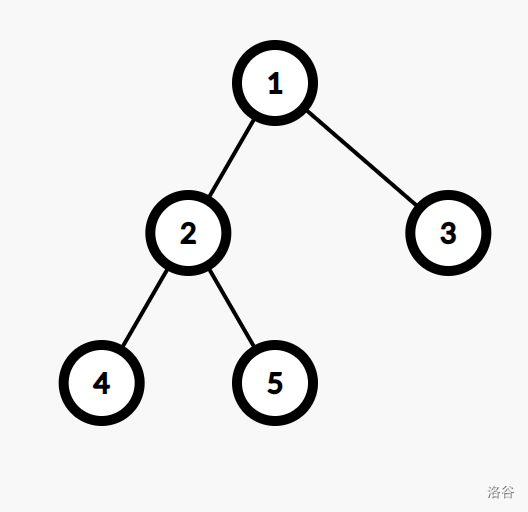
我们给出 数组:
显然,对于 ,如果 ,那么连边后最短路更新了,不能连。考虑到重边,我们只能额外连:
第 种的答案是 ,很好求。对于第 种,对于 ,除了自己父亲,上一层都有 条边与自己相连,因此答案是 。当然这里无限求 最大即可。
最后求和用快速幂求答案即可。
Code
#include <bits/stdc++.h> using namespace std; #define int long long int n,ans,dis[1000005],f[1000005],d[10000005]; vector<int> g[1000005]; void bfs() { queue<int> q; q.push(1); f[1] = 1; while (!q.empty()) { int u = q.front(); q.pop(); for (int v : g[u]) { if (!f[v]) { f[v] = 1; dis[v] = dis[u] + 1; q.push(v); } } } } int qpow(int a,int b,int p) { int res = 1; while (b != 0) { if (b % 2 == 1) res = res * a % p; a = a * a % p,b /= 2; } return res; } signed main() { ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); cin >> n; for (int i = 1,u,v;i < n;i++) { cin >> u >> v; u++,v++; g[u].push_back(v); g[v].push_back(u); } bfs(); int ma = INT_MIN,ans = 0; for (int i = 1;i <= n;i++) { d[dis[i] + 1]++; ma = max(ma,dis[i] + 1); } for (int i = 1;i < ma;i++) { ans = ans + (d[i] - 1) * d[i + 1]; } for (int i = 1;i <= ma;i++) { ans = ans + (d[i] * (d[i] - 1) / 2); } const int md = 1e9 + 7; cout << qpow(2,ans,md); return 0; } -
信息
- ID
- 151
- 时间
- 3000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 359
- 已通过
- 97
- 上传者